Regressão Linear Generalizada
Regressão linear generalizada, é uma versão generalizada do modelo de regressão linear que estima uma função linear que minimiza a distância entre os pontos do modelo à função usando uma distribuição para a função de perda genérica, não assumindo uma distribuição normal assim como na regressão linear.
Conectores
| Entrada | Saída |
|---|---|
| Dados utilizados para treinar o modelo | Dados de saída e Modelo do algoritmo de regressão |
Tarefa
Nome da Tarefa
Aba Execução
| Parâmetro | Detalhe |
|---|---|
| Atributo(s) previsor(es) | Atributo que será usado para treinamento |
| Atributo com o rótulo | Atributo a ser predito |
| Atributos com a predição | Atributo contendo a predição do modelo |
| Iterações máximas | Define o número máximos de iterações para a convergência do algoritmo, quanto maior mais iterações serão permitidas para encontrar a função linear para os dados, o valor padrão é 100 |
| Regularização | Valor para regularizar o fitting da função de perda do algoritmo, o valor padrão é 0 |
| Mix. para ElasticNet (entre 0 e 1) | Parâmetro de ajuste usado para a minimização da função objetivo usando uma combinação de L1 e L2. Valor por padrão é 0 |
| Família | Função de distribuição que representa a dispersão do modelo de predição, este é uma generalização da família de dispersão exponencial. |
| Link prediction | Parâmetro que gera a relação entre a predição linear e a média da função de distribuição do modelo |
| Parâmetro de regularização | Valor para regularizar o fitting da função de perda do algoritmo, esse parâmetro é usado para evitar overfitting, o valor padrão é 0 |
| Solucionador (Solver) | Algoritmo gera a solução da otimização do problema de regressão. Valor padrão dessa variável é auto |
| Métrica para validação cruzada | Define a métrica utilizada dentro da validação cruzada (se aplicável) para avaliar o modelo de classificação dentro das k partições |
| Atributo com o número da partição (fold) | Define o atributo a ter o número da partição para realizar uma validação cruzada (se aplicável) |
Exemplo de Utilização
Objetivo: utilizar os dados horsepower (cavalos de potência de cada carro) e o price (preço do carro) para estimar o preço a partir da potência do veículo.
Base de Dados: mtcars

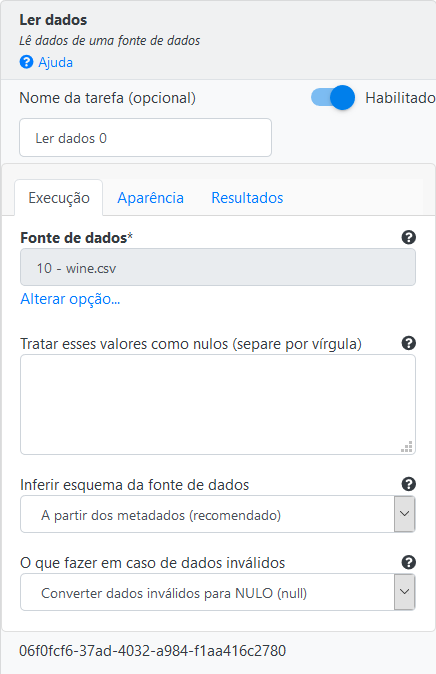
Adicione uma base de dados por meio da operação Ler dados.
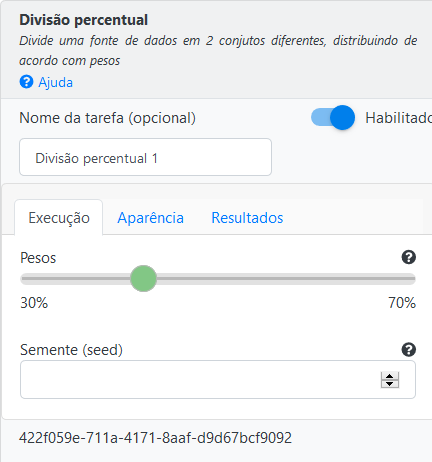
Usando a operação Divisão Percentual divida a base de dados em treino e teste utilizando uma distribuição de 70% para treino e 30% para teste.
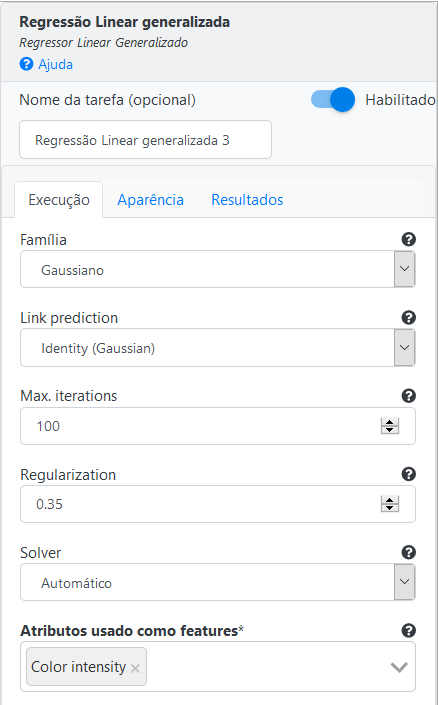
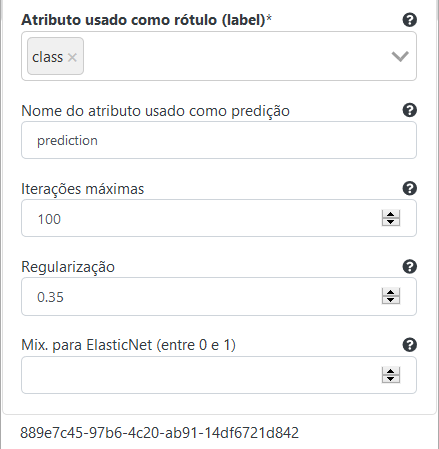
Na operação Regressão Linear Generalizado coloque o número de Iterações Máximas como 100, preencha 10 no campo Profundidade Máxima, deixe o valor de Solver como Auto e o parâmetro de regularização como 0.35. Use a função Gaussiana no campo Family como probabilidade de distribuição e a função de identidade no campo Link Prediction.
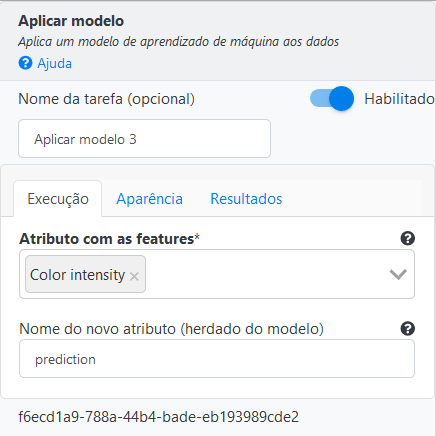
Na operação Aplicar Modelo, selecione *“Horse_Power” no campo Atributos com features e preencha “prediction” no campo Nome do novo atributo.
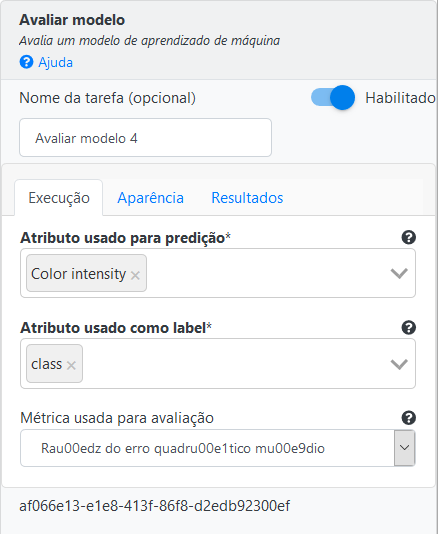
Na operação Avaliar Modelo, selecione “Price” no campo *Atributo usado para predição. Selecione “prediction” no campo Atributo usado como label. E selecione a métrica “Root Mean Square Error” como métrica para avaliação.
Execute o Fluxo e visualize o resultado.
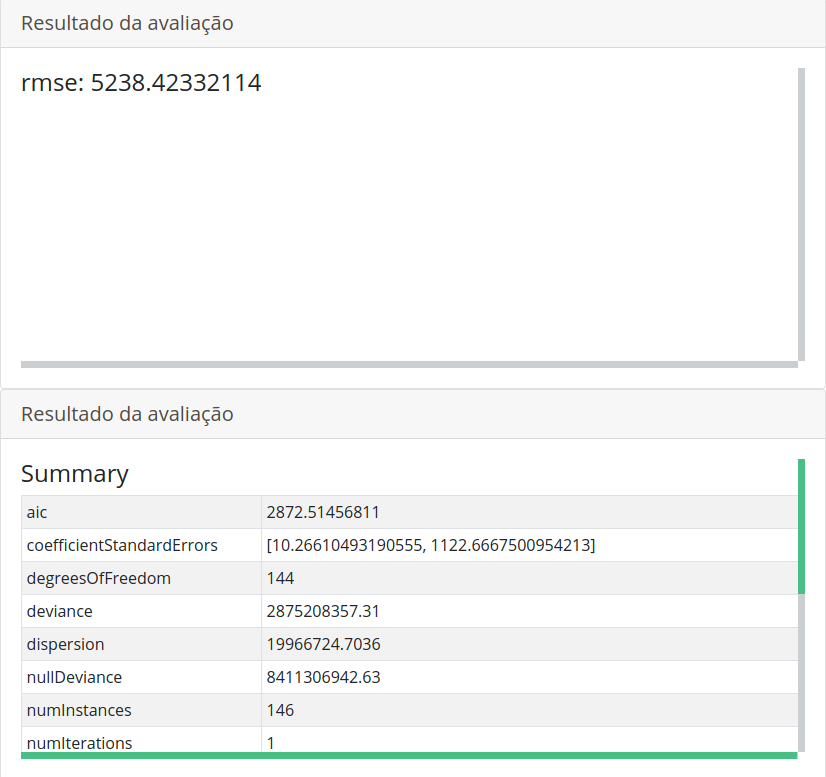
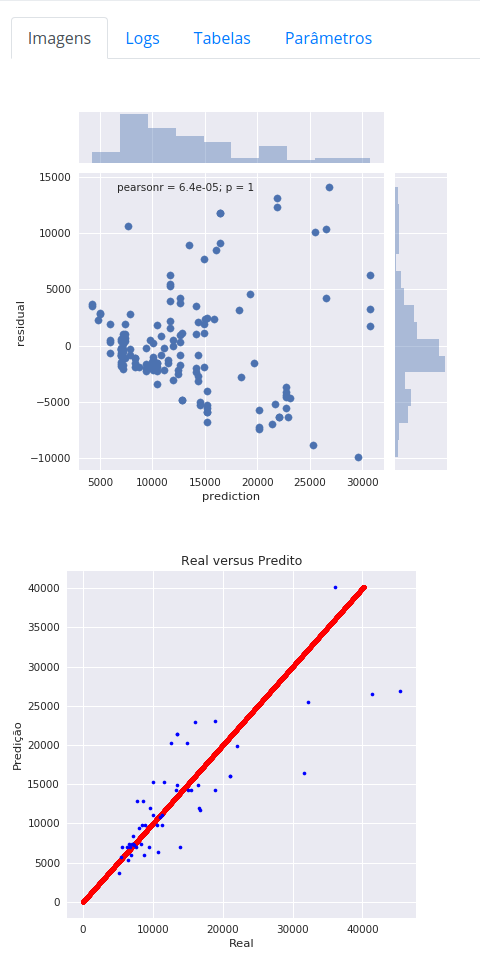
O valor predito é de 5238.423. No primeiro gráfico residual da predição que investiga o uso da do modelo de predição, podemos ver que a distribuição apresentada se adequa às suposições para o uso da regressão linear generalizada. No segundo gráfico vemos a distribuição dos dados reais que era desejado prever e a reta vermelha que representa a predição feita pelo modelo, podemos ver que a regressão encaixa bem nos dados desejados.
Dúvidas e/ou sugestões envie um e-mail para suporte@lemonade.org.br
